Statisztika, 16. tétel, pszichológia távoktatás
A próbafüggvények és típusai
(leírás, magyarázat)
Berei Kati által kidolgozva
Próbafüggvény
– A hipotézisek vizsgálatára hasznájunk
– mintáról mintára ingadozó jellemzők (vagyis a sokaságból vett minták megfelelő értékei nem véletlenszerűen, hanem függvényszerűen változnak)
– A próbafüggvényt úgy kell megválasztani, hogy
– a sokaságra tett bizonyos kikötések teljesüljenek
– a mintavétel adott módja és nagysága szerint
– feltételezzük a H0 helyességét
– ismert kell legyen a függvény valószínűségeloszlása: ehhez a H0 egyszerű hipotézis kell legyen.
Próbák lehetnek:
– egymintás próbák – olyan próbák, melyek elvégzéséhez elégséges egyetlen minta
– egymástól független minták vagy ún. páros minták lehetnek – amikor két vagy több minta szükséges, melyekről feltételezzük fel, hogy különböző sokaságokból származnak.
A HIPOTÉZISVIZSGÁLAT SORÁN HASZNÁLT PRÓBAFÜGGVÉNYEK
- Standard normális eloszlás
– a sokaságok egy jó része normális eloszlású – ezek próbafüggvényeit általában a standard (normális) eloszlás sűrűségfüggvényével írhatjuk le (ennek jellegzetes értékei táblázatban vannak, nincs szabad paraméter)
A leggyakoribb szignifikanciaszintekhez tartozó z-értékek:
| szignifikanciaszint α
% |
0,10
10% |
0,05
5% |
0,01
1% |
|
| egyoldali próba | jobb oldali | -1,28 | -1,6545 | -2,33 |
| baloldali | 1,28 | 1,6545 | 2,33 | |
| kétoldali próba | ± 1,6545 | ± 1,96 | ± 2,58 | |
Azért, hogy ne kelljen állandóan behelyettesítgetni a normál eloszlás sűrűségfüggvényébe az értékeket – standardizálták, vagyis megfosztották a mértékegységtől:
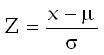
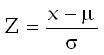
z – standard érték
x – függő változó
μ – átlag
σ – szórás
– a standard z érték egy egységnyi szórásnak felel meg
– a várt érték 0,
– egy adott z értékhez tartozó görbe alatti területek értékét táblázatba foglalták – ezeket megkapjuk vizsgán (ez a 3-as táblázat minden statisztikakönyv végén)
Standardizálás 1 példa
Egy diákcsoport IQ-átlaga 110, szórása pedig 15 pont volt. Határozza meg a 125, illetve a 90 pontú hallgató standard eredményét, s helyzetét!
50+34,13% Nálánál gyengébb vagy azonos eredményt 84,13% ért el.
-40,8 ~ 9% nálánál is gyengébb eredményt produkált.
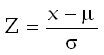
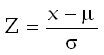
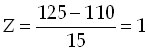
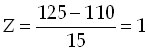
Standardizálás 2 példa.
Egy diákcsoport tesztátlaga 50, szórása pedig 20 pont volt. Határozza meg a 70, illetve a 45 pontú hallgató standard eredményét, s helyzetét!
50+34,13% Nálánál gyengébb vagy azonos eredményt 84,13% ért el.
-9,87%~ 40% nálánál is gyengébb eredményt produkált.
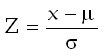
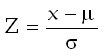
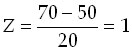
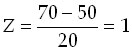
- Student féle t-eloszlás(sörgyári „megvilágosodás” ☺)
– egy normális és egy c négyzet eloszlású változó transzformáltjának hányadosából származtatható
– szimmetrikus a 0 pontra, a t-eloszlást egy paramétere, szabadságfok (ν) jellemzi.
– A szabadságfok növekedésével, vagy nagy minták esetén (n >100) a t-eloszlás egyre közelít a standard normális eloszláshoz.
– A Student-féle t-eloszlás táblázata a szabadságfok függvényében és a választott szignifikanciaszint szerint adja meg az elutasítási tartomány határát (értékeit megadják táblázatban vizsgán (a III. mellékletben vannak))
- Khi-négyzet eloszlás(más néven függetlenség ellenörzés)
– a khi-négyzet eloszlás paramétere a szabadságfok
– a görbe alatti területek egyaránt 1-gyel egyenlők, illetve a szabadságfok növekedésével az eloszlás mind jobban kezd hasonlítani a normális eloszláshoz
– megadják táblázatban (IV melléklet) az eloszlás percentiliseit a szabadságfok függvényében.
– ha a szabadságfok nagyobb mint 50, akkor a normális eloszlás táblázata is használható. (itt a tábla mérete a meghatározó!)
–
A c2 kétoldali 5%-os konfidenciahatárai tehát:
- Fisher féle F-eloszlás
– A kétmintás próbák elemzésekor a két minta átlagainak különbsége mellett fontos a két minta varianciájának a vizsgálata is
– Ha a sokaság (közel) normális eloszlású, akkor a belőle vett két-két minták varianciájának a hányadosa egy bonyolult újabb eloszlást eredményez.
– Az V. Melléklet mutatja az F-eloszlás leggyakrabban használt, 95-ödik percentilis értékeit a minták szabadságfokának függvényében.
Meghatározás:
, ahol 
a korrigált szórás, N a minták korrigált szórása
–
Amennyiben az F-eloszlást a statisztikai próbáknál a populációk varianciájának összehasonlítására kívánjuk felhasználni, az a nullhipotézisünk, hogy a két variancia megegyezik, azaz:
ilyenkor az F-eloszlás képlete tovább egyszerűsödik:
A tört képzésekor rendszeresen a nagyobb empirikus szórásnégyzetet jelöljük s12-el és azt osztjuk el az alacsonyabb értékű s22-vel.
A szabadságfok
– Mind a t-, mind a c -négyzet kiszámításához a mintából kapott és bizonyos sokasági paraméterek szükségesek
– szabadságfok (nű) kiszámításához: a mintanagyságból (N) levonjuk a mintából becsülni kívánt paraméterek (k) számát: ν = N–k.
– A t-statisztika esetében az N számú elemből kiszámíthatjuk a mintaátlagot és -szórást.
– c négyzetnél a mintából számítható annak szórása – a gyakorlatban a kontingenciatábla méretéből származtatjuk az eloszlás szabadságfokát.
(Kicsit sántító, de képszerű példa a szabadságfok fogalmára: 10 vendéget várunk, ezért kikészítünk 10 széket; az elsőként megérkező vendég választhat, melyik székre ül le. Még a kilencediknek érkező vendég is választhat a szabadon levő két szék közül, de a tízedik vendégnek már nincs szabadság(fok)a a szék megválasztásában, hiszen már csak egyetlen egy üres.)
A mellékletekben kévő táblázatok az elektronikus konyvtárban a Statisztika ablak cím alatt vannak!
Megjegyzés: nem minden képet sikerült beszúrni… 🙁