Statisztika, 3. tétel, pszichológia távoktatás
Átlag és szórás (számítás)
Berei Kati által kidolgozva
A sokasági adatok tömör jellemzésére használjuk a középértékeket – vagyis az adatok halmazának a középtáján elhelyezkedő érték amely jellemző az adatok sokaságára és segít sűríteni és könnyebben feldolgozni az adathalmazt.
Átlag – ez az általánosan használt számított középérték ami alatt a számtani átlagot érjük, de használunk harmonikus, mértani és négyzetes átlagot is.
Számtani átlag
– Az x1, x2, x3, … xn számhalmaz számtani átlagát úgy számítjuk, hogy az értékeket összeadjuk, s az összeget elosztjuk az elemek számával. Az átlagértéket a változójel felülhúzásával jelöljük:


Pl. a 6, 3, 4, 4, 8, 8, 10, 5, 3, 4, 4 számok átlaga:
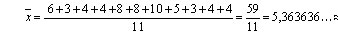
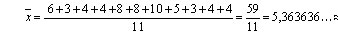
Ha számhalmazban több azonos értékű is van – az x1 f1-szer, az x2 f2–szor … az xn fn-szer fordul elő, akkor a számtani átlag képlete így alakul:
Az előző példában a 3 és a 8 kétszer, a 4 négyszer, az 5, 6 és a 10 egyszer-egyszer szerepel, tehát:
Súlyozott számtani átlag
Ha az átlagolandó értékek közül némelyiket valamilyen ok (fontosság, jelentőség, pl. egy vizsga háromszor annyit ér, mint egy házidolgozat), akkor w1,w2,w3,…wn súlyokat rendelünk az átlagolandó x1, x2, x3, … xn értékekhez, és súlyozott számtani átlagnak nevezzük:
Harmonikus átlag
– általában teljesítmények átlagolására használjuk (átlagsebesség)
– úgy számolunk, hogy az átlagolandó értékek reciprokát összegezzük (vagyis közös nevezőre hozzuk), majd az elemszámot osztjuk ezzel a reciprok-összeggel
– megkülönböztetéséül a számtani átlagtól, az alsó indexbe helyezett h–karakterrel jelöljük:
súlyozott alakja:
Pl: a Bp- Pécs távolság 210 km. Ebből 70 km autópálya (130 km/h), másik 70 km-t 90 km/h, a maradék 70 km-t 50 km/h sebességgel haladtunk, akkor a teljes útra vonatkozó átlagsebességünk nem , hanem:
Mértani (geometriai) átlag
– meghatározás szerint:
N számú pozitív szám mértani átlaga – a számok szorzatának N-edik rendű gyöke, nem nagyon használt
– pl. láncviszonyszámok átlagát számolhatjuk vele:
(láncviszonyszám: idősoroknál minden egyes év adatát az azt megelőző időszak adatához viszonyítjuk, megmutatja a változás dinamikáját)
Négyzetes átlag
– kedvelt a statisztikában is mert a négyzetre emelés „megszünteti” a mínusz előjelet – ez a tulajdonság – az előjel kiküszöbölése – fontos a szórás számításakor:
Pl. Egy vadász azt mondja feleségének: asszony, nyúlpaprikást főzzél! Igaz, hogy egyszer jobbra lőttem mellé egy méterrel a nyúlnak, egyszer pedig balra egy méterrel, de statisztikai értelemben az a nyúl el van ejtve. Az asszony azonban tanult némi statisztikát, s kioktatta férjét, hogy adott esetben nem a számtani átlag, hanem a négyzetes átlag jöhet szóba, a nyúlpaprikásról pedig szó se essék.
Magyarázat:
– +2 és -2 négyzete egyaránt +4, a gyökvonás két gyököt eredményez? a gyök 4 = -2 vagy +2, de a statisztikában eltekintünk a negatív előjelű gyöktől.
– Ha a (+1) és a (-1) az átlagolandó értékünk, akkor azok számtani átlaga 0: (1-1)/2=0/2=0.
–
A négyzetes átlag már jobban utal arra, hogy nem két 0 vagy két abszolút értékben azonos szám átlaga a 0:
Szórás, variancia
– az átlag nem ad felvilágosítást arról, hogy a kiinduló adatok mennyire különböztek egymástól. Tehát olyan statisztikai mutatókat kell használni, amik az adatok szóródását, változékonyságát mutatják, ilyen a szórás.
Pl.2 magyarországi diáknak lehet egyaránt közepes az átlageredménye a szemeszter végén, ám egyiknek 3, 3, 3, 3, 3 áll az indexében (megbízhatóan közepes teljesítmény), a másiknak 1, 2, 2, 5, 5 az osztályzatai ugyanazon tárgyakból (2 tárgyból is kiváló, tehetséges, a többinél lusta). A két diák közötti különbséget a számtani átlag önmagában eltünteti.
– A leggyakrabban használt a szórás és ennek négyzete, a variancia
Szórás
– a számtani átlagtól vett eltérések négyzetes átlaga
– jele a görög kis szigma (s), ha a szórás a sokaság szórása és s betű a részsokaság vagy a sokaságból vett minta szórása:
Variancia – a szórás négyzete, jelölése s2, ha sokasági, s2 ha mintából számított:
Pl. annak a diáknak akinek mind az öt vizsgaeredménye közepes volt (3, 3, 3, 3, 3) annak nyilván 0 a jegyeinek szórása. Az átlaga 3, tehát:
A másik diák (1, 2, 2, 5, 5) átlaga szintén közepes (3), de a jegyeinek szórása már nem 0:
Számítógépen az Excel programban: szórás – a szórásp (stdevp), variancia – a varp (varp), átlag – az átlag (average) függvénnyel számíthatjuk.
