Statisztika, 10. tétel, pszichológia távoktatás
Kapcsolatvizsgálatok (Yule-próba, khi-négyzet próba)
(számítás)
Berei Kati által kidolgozva
Asszociációs kapcsolatban használjuk:
- alternatív kapcsolat esetén – két-két ismérv van – Yule-mutatót
- kettőnél több ismérv-változat esetén – khi-négyzet próbát
Yule-féle asszociációs együttható
A kontingenciatábla:
| Csoport | B1 | B2 |
| A1 | f11 | f12 |
| A2 | f21 | f22 |
A Yule Mutató


Tulajdonságok: –1 £ Y £ 1
– függetlenség esetén Y = 0 (fordítva nem igaz! Előfordulhat ugyanis, hogy az noha különböző értékek vannak a cellákban Az f11×f22 szorzat értéke megegyezik az f21×f12-ével.)
– függvényszerű kapcsolat esetén ïYï = 1 (fordítva nem igaz! Lehet ugyanis olyan táblázatunk, amelyben az egyik cella értéke nulla, azzal 0 lesz azon szorzatpár értéke is)
– sztochasztikus kapcsolat esetén 0 < ïYï < 1
– Y > 0 ha f11f22 > f21f21 vagyis az azonos indexek jobban vonzzák egymást.
A Yule-próba hibái:
– ha az egyik cella értéke 0 megtévesztő, függvényszerű kapcsolatot is kimutathat (Y=1)
– ha két szorzat értéke ugyanaz, nem alkalmas a szorosság kimutatására (Y=0)
Khi – négyzet próba c2
Akkor használjuk ha:
– ha fenti okok miatt nem felel meg a Yule-mutató
– ha ismérvenként több osztály van, vagyis nagyobb a kontingencia-táblázatunk
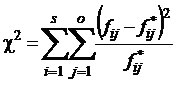
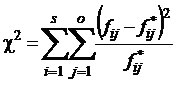
![]()
![]()
Tulajdonságok:
→ 0 £ c2 £ N min(s-1, t-1)
→ c2 = 0 akkor és csak akkor, ha a két ismérv független
→ c2 = N (s-1) akkor és csak akkor, ha a két ismérv függvénykapcsolatban áll, ekkor s=t
Egyszerűbben:
– ha c2 = 0, akkor nincs összefüggés a csoportképző ismérvek között
– ha c2 ≠ 0, akkor feltételezhető a kapcsolat
A c2 mutató azonban csak áttételesen utal a kapcsolat szorosságára, mivel nem elégíti ki a valószínűségi mutatóval szemben állított azon követelményt, hogy értéke nulla és egy közé essen.
Két eljárás is van a c2 valószínűségi mutatóvá alakítására.
A Csuprov-féle asszociációs együttható (T)
– a kontingenciatábla nagyságával és a teljes elemszámmal viszonyítja a khi-négyzet mutatót:
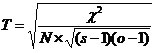
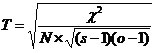
, ahol s – sorok száma, o – oszlopok száma
A Cramer-féle asszociációs együttható
– hasonló módon alakítja át a khi-négyzet mutatót, de a táblanagyságból csak a kisebb osztályszámú sort vagy oszlopot veszi figyelembe:


Cramer-féle asszociációs együttható tulajdonságai:
→ ha s = o, akkor C = T
→ C = 0 akkor és csak akkor, ha a két ismérv független
→ C = 1 akkor és csak akkor, ha a két ismérv között függvénykapcsolat áll fenn.
35% -gyenge
35-70% közepes
70% fölött szoros kapcsolat

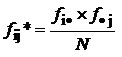
Ezer köszönet az oldalért, ez a legjobban összerakott és elmagyarázott tétel, amit eddig találtam!!!!!